Given a m*n matrix with sorted rows and columns. Search a given element “x” in the matrix and return “true” for successful search otherwise return “false” , provided with the condition that first integer in each row is greater than the last integer of the previous row.
Video explanation of the solution approaches for this problem can be found in the below link:
https://www.youtube.com/watch?v=gUc92h0SeO8&t=7s
Possible Examples:
Before jumping directly to the solution approaches, lets discuss about the possible inputs and their respective outputs.
i/p:
[
[1,2,3],
[4,5,6],
[7,8,9]
]
x = 2
o/p:
true
i/p:
[
[21,32,33],
[44,45,46],
[67,68,69]
]
x = 89
o/p:
false
i/p:
[]
x = 8
o/p:
false
public boolean searchIn2dArray(int[][] matrix, int x){
// code your approach here
}
Solution Approach 1 (Brute Force Approach) :
For this approach, run two loops covering all the elements of rows and columns and compare whether the element to be searched is same as the current element of the iteration. If the search is successful, return true. If the iteration is completed, then return false. This depicts none of the elements in the array matched with the element to be searched.
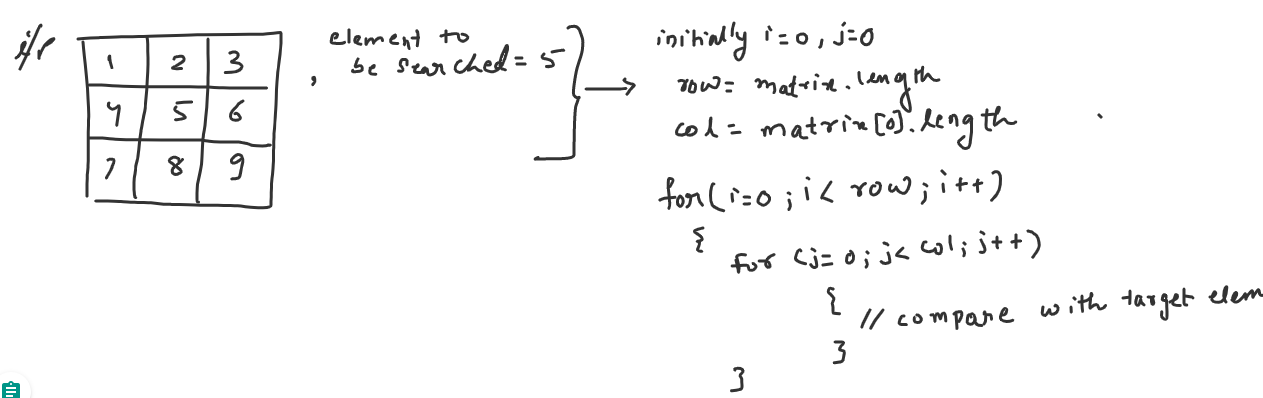

Complexity Analysis:
Time Complexity : For each row, we have to compare all the column elements. In the worst case, the time require to search an element is m*n where m is row length and n is column length.
Hence T(n) = O(m*n).
Space Complexity : As we have not used any extra space to perform search operation, hence S(n) = O(1)
Can we optimize it further?
Yes.
Solution Approach 2 ( Making use of any one Condition : Rows are Sorted or Columns are sorted)
For all the m rows, perform binary search for each row. Detailed description of binary search can be found in the above provided link.
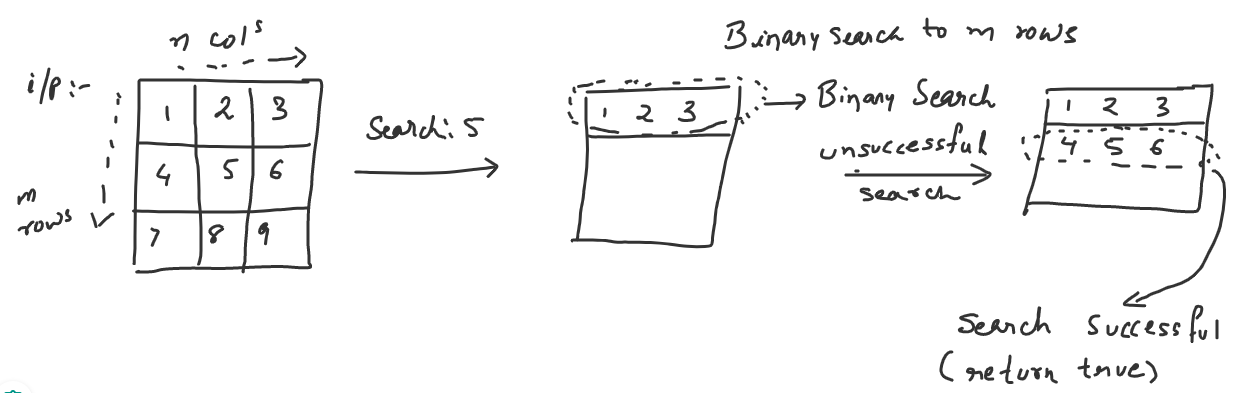
In any of the iteration, return true for the successful search and return false if check is performed with all row elements.
Complexity Analysis:
Time Complexity: Each row contains n elements and time complexity to search an element using binary search approach is O(log n). But for this problem, we are performing binary search for m rows, hence time complexity will be O(mlogn).
If search is performed column wise, so the time complexity will be O(nlogm).
Hence, overall time complexity is T(n) = O(nlogm+mlogn)
Space Complexity : As we have not used any extra space to perform search operation, hence S(n) = O(1)
Solution Approach 3 (Make use of both the condition : Rows and Columns are Sorted)
Lets start searching the given element from the right most index i.e. matrix[0][n-1]. So there are three possibilities encountered:
- Element to be searched is same as matrix[0][n-1]
- Element to be searched is greater than matrix[0][n-1]
- Element to be searched is less than matrix[0][n-1]
Lets understand all the cases with the given example:
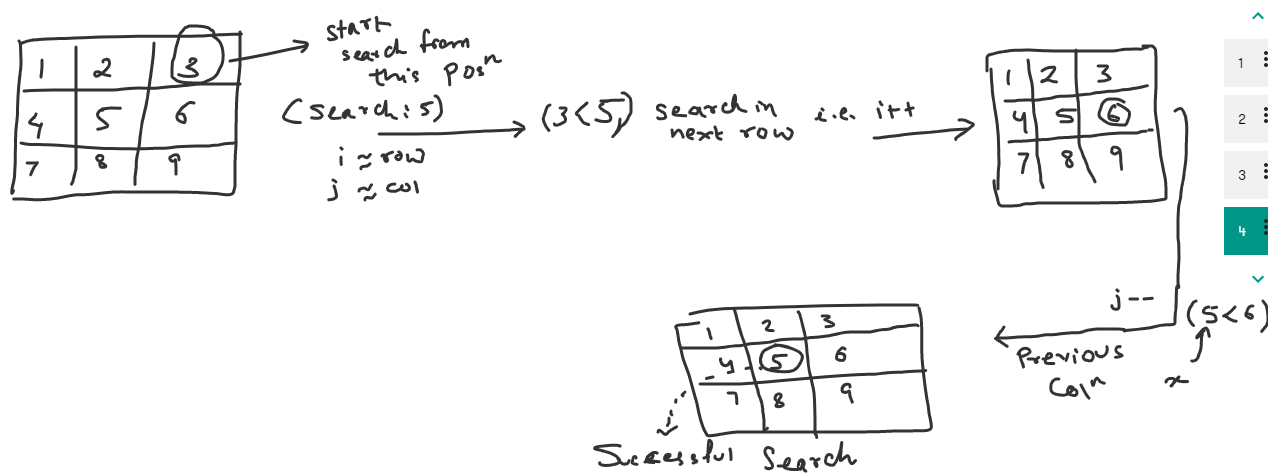
Lets take an example where search is unsuccessful :
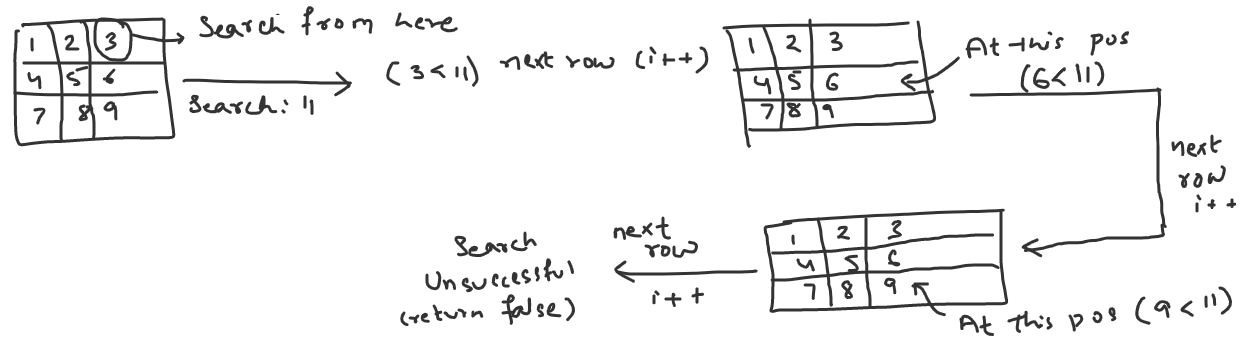
Complexity Analysis:
Time Complexity: For this approach, either we are eliminating row or column based on the element to be searched. Hence the time complexity is O(m+n).
Space Complexity : As we have not used any extra space to perform search operation, hence S(n) = O(1)
You can find the full code here: SearchIn2dArray
I hope the different solution approaches will help to enhance your problem solving capability. Let me know your thoughts in the comment section.
Happy Coding Aspirants and Good luck for your interviews!!!
